พีชคณิตแบบบูล ส่วนที่ 2 กฎหมายและฟังก์ชันพื้นฐาน

ความต่อเนื่องของเรื่องราวเกี่ยวกับพีชคณิตแบบบูลอนุสัญญากฎการดำเนินงาน เปลี่ยนเป็นพื้นฐานของวงจรสัมผัส

บทความแรก George Bull ถูกอธิบายว่าเป็นผู้สร้างพีชคณิตของตรรกะ บทความที่สองจะอธิบายการทำงานพื้นฐานของพีชคณิตแบบบูลและวิธีการในการทำให้นิพจน์บูลีนเป็นเรื่องง่าย ดังนั้นพีชคณิตแบบบูลใช้ข้อความเป็นข้อโต้แย้งไม่ใช่ความหมาย แต่เป็นความจริงหรือความเท็จของข้อความ

แบบฟอร์มสำหรับการเขียนนิพจน์ในพีชคณิตแบบบูล

ถ้าข้อความนั้นเป็นจริงมันจะถูกเขียนเช่นนี้: A = 1 ถ้ามันเป็นเท็จ A = 0 (หลังจากทั้งหมดมันไม่เป็นความจริงเลยว่ามันฝรั่งเป็นผลไม้) สำหรับข้อความใด ๆ A จะเป็นจริง (A = 1) หรือเท็จ (A = 0) ที่นี่ไม่มีตรงกลาง เราได้พูดคุยเกี่ยวกับเรื่องนี้แล้ว

หากคุณเชื่อมต่อสองคำสั่งง่ายๆกับสหภาพและคุณจะได้คำสั่งที่ซับซ้อนซึ่งเรียกว่าผลิตภัณฑ์เชิงตรรกะ ลองทำสองคำง่ายๆ:“ สามมากกว่าสอง” เราจะกำหนดด้วยตัวอักษร A,“ สามน้อยกว่าห้า” - ตามตัวอักษร B

ดังนั้นคำสั่งที่ซับซ้อน“ สามมากกว่าสองและน้อยกว่าห้า” จึงเป็นตรรกะหนึ่ง (ในกรณีนี้อักษรตัวใหญ่และบอกว่านี่คือการดำเนินการทางตรรกะ“ AND” รวมถึงในภายหลังในข้อความ“ หรือ” และ“ ไม่”) และ B มันถูกกำหนดดังนี้: A ^ B หรือ A * B

การคูณเชิงตรรกะ (การดำเนินการ "AND")

ในพีชคณิตระดับประถมศึกษา A * A = A2 แต่ในพีชคณิตของ Buhl A * A = A2 = A, A * A = A เนื่องจากเครื่องหมายการคูณ (*) ตอนนี้หมายถึง ... และ ... ในแง่ของ And ... และ ประสบการณ์ทั้งหมดของเรายืนยันว่า A&A เหมือนกับ A. เพียงอย่างเดียวไม่มีใครไม่เห็นด้วยกับสิ่งนี้ ความจริงของคำสั่งจะไม่เปลี่ยนแปลงหากมีการทำซ้ำโดยปัจจัยหลายครั้ง

ผลิตภัณฑ์ของสองประโยคถือว่าเป็นจริง (เท่ากับ 1) จากนั้นและเฉพาะในกรณีที่ปัจจัยทั้งสองเป็นจริงและเท็จ (เท่ากับ 0) หากอย่างน้อยหนึ่งในปัจจัยนั้นเป็นเท็จ ยอมรับว่ากฎเหล่านี้ไม่ขัดแย้งสามัญสำนึกและนอกจากนี้พวกเขาปฏิบัติตามกฎของพีชคณิตเบื้องต้นอย่างเต็มที่:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

ความเท่าเทียมกันครั้งแรกอ่านดังนี้: ถ้าทั้ง A และ B เป็นจริงดังนั้นผลิตภัณฑ์ A * B จะเป็นจริง ในพีชคณิต Buhl เครื่องหมายการคูณ (*) แทนที่ union I.

ผลิตภัณฑ์เชิงตรรกะอาจรวมถึงไม่สอง แต่เป็นจำนวนงบที่มากขึ้น - ปัจจัย และในกรณีนี้ผลิตภัณฑ์เป็นจริงเฉพาะเมื่อในเวลาเดียวกันทุกปัจจัยงบเป็นจริง

การเพิ่มตรรกะ (หรือการดำเนินการ)

หากสองคำสั่งมีการเชื่อมต่อโดยสหภาพหรือ ประโยคประกอบที่เกิดขึ้นนั้นเรียกว่าผลรวมเชิงตรรกะ

ลองพิจารณาตัวอย่างของผลรวมเชิงตรรกะ บอกว่า: "วันนี้ฉันจะไปดูหนัง"

ถ้อยแถลง B:“ วันนี้ฉันจะไปดิสโก้” เราเพิ่มทั้งสองข้อความและรับ: "วันนี้ฉันจะไปดูหนังหรือไปที่ดิสโก้"

คำสั่งที่ซับซ้อนนี้ถูกเขียนแทนดังนี้: A + B = C หรือ (A V B) = C

โดย C เราแสดงถึงคำสั่งที่ซับซ้อนของผลรวมทางตรรกะ

ในตัวอย่างภายใต้การพิจารณาสหภาพหรือไม่สามารถใช้ในความหมายพิเศษ แน่นอนในวันเดียวกันคุณสามารถไปที่โรงภาพยนตร์และดิสโก้ได้ และนี่คือคำพูด:

“ ประธานหุ้นส่วนการทำสวนจะเปตรอฟหรืออิวานอฟ” - ไม่ใช่ผลรวมเชิงตรรกะเพราะมีเพียงคนเดียวเท่านั้นที่จะเป็นประธานและอีกคนจะเป็นนักสวนมือสมัครเล่นทั่วไป

เลือกสัญลักษณ์ V สำหรับผลรวมทางตรรกะเนื่องจากเป็นตัวอักษรเริ่มต้นของคำภาษาละติน "vel", ความหมาย "หรือ" ตรงกันข้ามกับคำภาษาละติน "aut> ซึ่งหมายถึง" และ " ตอนนี้มันควรจะชัดเจนสำหรับทุกคนว่าทำไมผลิตภัณฑ์ลอจิคัลถูกระบุโดยเครื่องหมาย ^

ในพีชคณิตเบื้องต้นมีกฎ A + A = 2A กฎนี้เป็นความจริงไม่ว่าตัวเลข A จะถูกแทนด้วยตัวอักษร A ในพีชคณิตแบบบูลกฎ A + A = A นั้นสอดคล้องกับประสบการณ์ชีวิตทั้งชีวิตของเราบอกว่าการบอกว่า A หรือ A หรือ A ทั้งสองเป็นเพียงอีกวิธีหนึ่ง

เช่นเดียวกับคำสั่งผสมใด ๆ ผลรวมของทั้งสองคำสั่ง A และ B สามารถเป็นจริงหรือเท็จ ผลรวมถือว่าเป็นความจริงนั่นคือเท่ากับความสามัคคีหากอย่างน้อยหนึ่งในเงื่อนไขเป็นจริง:

A + B = 1 ถ้า OR A = 1 หรือ B = 1 ซึ่งสอดคล้องกับเลขคณิตทั่วไป:

1+0 = 0+1 = 1.

หากข้อความทั้งสองข้อสรุปเป็นจริงดังนั้นผลรวมก็ถือว่าเป็นจริงดังนั้นในพีชคณิตบูลีนเรามี: (1) + (1) = 1

วงเล็บถูกตั้งไว้ที่นี่เพื่อเน้นเงื่อนไขเงื่อนไขความหมายของการเพิ่มนี้ไม่ใช่คณิตศาสตร์

ผลรวมของสองคำสั่งถือเป็นเท็จและเท่ากับศูนย์ถ้า แต่เฉพาะถ้าทั้งสองคำเป็นเท็จ จากที่นี่:

0 + 0=0.

ดังนั้นผลรวมของทั้งสองประโยค A + B จึงถือว่าเป็นจริงหากเป็นจริงหรือ A, หรือ B หรือทั้งสองคำรวมกัน ดังนั้นคำหรือถูกแทนด้วย +

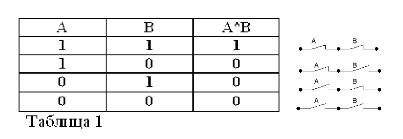
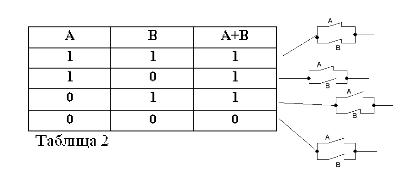
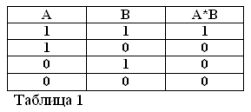
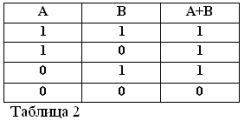
การจดจำว่าคำสั่ง A และ B สามารถเป็นจริงหรือเท็จเท่านั้นและดังนั้นจึงมีการวัดความจริง 1 หรือ 0 ผลลัพธ์ของการดำเนินการ AND และ OR ที่พิจารณาสามารถสรุปได้ในตารางที่ 1 และ 2

การดำเนินการที่สามซึ่งใช้กันอย่างแพร่หลายโดยพีชคณิตแบบบูลคือการลบล้าง - ไม่ใช่ เราเตือนคุณว่าพีชคณิตเบื้องต้นใช้การดำเนินการ ADD, D Subtract, คูณด้วยหารด้วยและอื่น ๆ

สำหรับแต่ละคำสั่ง A มีการปฏิเสธไม่ใช่ A ซึ่งเราจะแทนด้วยสัญลักษณ์ / A สิ่งนี้ไม่น่าสงสัย

เรายกตัวอย่าง:“ เราจะไปที่ป่า” A,“ เราจะไม่ไปที่ป่า” / A.

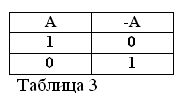
หากข้อความ A เป็นจริงนั่นคือ A = 1 ดังนั้นการปฏิเสธ / A จะต้องเป็นเท็จ / A = 0 และในทางกลับกันหากข้อความใด ๆ เป็นเท็จการปฏิเสธของมันเป็นความจริง ตัวอย่างเช่น:“ ม้าไม่กินหญ้าแห้ง” / A = 0,“ ม้าไม่กินหญ้าแห้ง” (A = 1) สามารถแสดงในตารางที่ 3

การพิจารณาความหมายของการกระทำของการปฏิเสธและสมมติว่าทั้งสองประโยค A และ / A นั้นเป็นจริงเสมอหนึ่งสูตรใหม่สองสูตรของพีชคณิตบูลีนจะเป็นดังนี้:

A + (/ A) = 1 และ A * (/ A) = 0

นอกจากนี้ยังมีสูตรอื่น ๆ ที่ทำให้การประมวลผลคำสั่งง่ายขึ้น ตัวอย่างเช่น 1 + A = 1 เนื่องจากตามคำจำกัดความของการเพิ่มในกรณีที่หนึ่งเทอมเท่ากับความสามัคคีผลรวมจะเท่ากับความสามัคคีเสมอ ผลลัพธ์ที่ได้ไม่ขึ้นอยู่กับว่า A = 0 หรือ A = 1

การดำเนินการเชิงตรรกะสามอย่างที่เราตรวจสอบ (และ, หรือ, ไม่) มีคุณสมบัติบางอย่างที่ใกล้เคียงกับกฎของพีชคณิตเบื้องต้น ถ้าพวกมันทั้งหมดถูกสร้างขึ้นมาเราจะได้กฎพีชคณิตบูลีน 25 ข้อ พวกเขาเพียงพอที่จะแก้ปัญหาเชิงตรรกะได้เกือบทั้งหมด หากปราศจากกฎเหล่านี้จะเป็นการยากที่จะแก้ปัญหาเชิงตรรกะเนื่องจากความซับซ้อนที่ชัดเจน การพยายามค้นหาคำตอบที่ถูกต้องโดยไม่ใช้กฎหมายถึงการแทนที่ด้วยความเฉลียวฉลาดและการใช้เหตุผลทั่วไป กฎช่วยอำนวยความสะดวกในการทำงานนี้อย่างมากและประหยัดเวลา

ภายในกรอบของบทความมันเป็นไปไม่ได้ที่จะต้องพิจารณากฎทั้ง 25 ข้อนี้ แต่ผู้ที่ต้องการสามารถพบพวกเขาได้เสมอในวรรณกรรมที่เกี่ยวข้อง

ดังกล่าวแล้วในบทความแรกในปี 1938 นักวิทยาศาสตร์หนุ่มชาวอเมริกัน Claude Shannon ในบทความของเขา "การวิเคราะห์เชิงสัญลักษณ์ของการถ่ายทอดและวงจรการสลับ" เป็นครั้งแรกที่ใช้พีชคณิตแบบบูลสำหรับปัญหาของเทคโนโลยีการถ่ายทอด การค้นพบของแชนนอนก็คือเขารู้ว่าวิธีการออกแบบเครื่องถ่ายทอดสัญญาณและคอมพิวเตอร์อิเล็กทรอนิกส์เป็นสาขาคณิตศาสตร์เชิงตรรกะ

มันมักจะเกิดขึ้น เป็นเวลาหลายปีที่นักวิทยาศาสตร์ได้ทำงานกับปัญหาที่ดูเหมือนไม่จำเป็นสำหรับเพื่อนร่วมชาติของเขา - เพียงแค่สนุก แต่ทศวรรษที่ผ่านมาและบางครั้งผ่านไปหลายศตวรรษและทฤษฎีที่ไม่มีใครต้องการไม่เพียง แต่ได้รับสิทธิ์ในการดำรงอยู่ แต่หากไม่มีความคืบหน้าต่อไป

อะไรช่วยให้แชนนอนเป็นครั้งที่สอง“ ค้นพบ” พีชคณิตแบบบูล? กรณี? ไม่มีอะไรชนิด

ความรักของเครื่องถ่ายทอดที่สร้างขึ้นจากสวิตช์และรีเลย์แบบเดิมช่วยให้นักวิทยาศาสตร์หนุ่มเชื่อมต่อทฤษฎีที่ถูกลืมกับงานแลกเปลี่ยนโทรศัพท์อัตโนมัติซึ่งเขาทำงานในเวลานั้น ต่อมาแชนนอนได้แนะนำแนวคิดเดียวกันว่า“ ใช่หรือไม่ใช่” ในข้อความที่ไม่ต่อเนื่องและวางรากฐานสำหรับไซเบอร์เนติกส์ทั้งหมด - ทฤษฎีสารสนเทศ

พีชคณิตของ Buhl เหมาะมากสำหรับการวิเคราะห์และสังเคราะห์วงจรรีเลย์ มันก็เพียงพอที่จะยอมรับว่าเป็นคำสั่งที่แท้จริง:“ มีสัญญาณในวงจร” และในฐานะที่เป็นเท็จ -“ ไม่มีสัญญาณในวงจร” เมื่อมีพีชคณิตใหม่ปรากฏขึ้น - พีชคณิตสัญญาณ, พีชคณิตวงจรรีเลย์

พีชคณิตใหม่มีผลเฉพาะเมื่อพิจารณาวงจรรีเลย์และสวิตช์ ท้ายที่สุดเพียงแค่ในรูปแบบดังกล่าวเป็นเงื่อนไข“ มีสัญญาณ” และ“ ไม่มีสัญญาณ” พอใจ ในกรณีที่สัญญาณมีการเปลี่ยนแปลงอย่างต่อเนื่องการรับเงื่อนไขกลางจำนวนมากโดยพลการ (สัญญาณดังกล่าวเรียกว่าอนาล็อก) ไม่สามารถใช้พีชคณิตรีเลย์ได้ สิ่งนี้จะต้องได้รับการจดจำเสมอ แต่คอมพิวเตอร์อิเล็กทรอนิกส์และเครื่องไซเบอร์เนติกส์ส่วนใหญ่ใช้หลักการประมวลผลสัญญาณแบบแยกซึ่งใช้องค์ประกอบ "ใช่ - ไม่ใช่"

นิพจน์ "ติดต่อปิด" ได้รับการยอมรับโดยแชนนอนว่าเป็นจริง (1) และ "ติดต่อเปิด" เป็นเท็จ (0) ส่วนที่เหลือของ "พีชคณิต" รวมถึงการดำเนินการ AND, OR และ NOT และ 25 กฎนอนส์ยืมมาจาก Boole

พีชคณิตวงจรรีเลย์กลับกลายเป็นว่าง่ายกว่าพีชคณิตบูลีนเนื่องจากเกี่ยวข้องกับองค์ประกอบของประเภท "ใช่ - ไม่ใช่" เท่านั้น นอกจากนี้พีชคณิตใหม่ยังมีความชัดเจนมากขึ้น

องค์ประกอบในพีชคณิตนี้คือที่ติดต่อซึ่งเราจะแสดงด้วยตัวอักษร A, B, C ... ผู้ติดต่อถูกปิด - A ผู้ติดต่อนั้นเปิดอยู่ - / A (ตัวอักษรที่มีเส้นประ)

สัญกรณ์อย่างที่คุณเห็นนั้นมาจากพีชคณิตบูลีน ผู้ติดต่อที่เปิดอยู่คือการปฏิเสธของผู้ติดต่อที่ปิด ผู้ติดต่อรายเดียวกันไม่สามารถปิดและเปิดได้

ขอให้เราตกลงกันว่าถ้าในวงจรใด ๆ สองรายชื่อจะแสดงด้วยตัวอักษรเดียวกันนั่นหมายความว่าพวกเขาจะใช้ค่าเดียวกันเสมอ

ในเวลาใดก็ตามพวกเขาทั้งสองเปิดในเวลาเดียวกันหรือทั้งสองอย่างถูกปิด วิธีที่ง่ายที่สุดในการจินตนาการว่าพวกเขาเชื่อมต่อกันด้วยกลไกเพื่อให้ทั้งคู่เปิดหรือปิดพร้อมกัน

หากในบางเชนผู้ติดต่อเป็นการปฏิเสธผู้ติดต่อรายอื่นความหมายของพวกเขาจะตรงกันข้ามกันเสมอ ตัวอย่างเช่นผู้ติดต่อ C และ / C ไม่สามารถเปิดหรือปิดพร้อมกันได้ และในแผนภาพพวกเขาสามารถเป็นตัวแทนของการเชื่อมต่อทางกลไก: ถ้าหนึ่งในนั้นเปิด

เราเริ่มทำความรู้จักกับพีชคณิตรีเลย์โดยการวิเคราะห์วงจรที่ง่ายที่สุดที่สอดคล้องกับการดำเนินการ AND, OR และ NOT

ผลิตภัณฑ์ของสองหน้าสัมผัส (การทำงาน AND) คือวงจรที่ได้รับจากการเชื่อมต่อแบบอนุกรม: มันถูกปิด (เท่ากับ 1) เฉพาะเมื่อปิดทั้งสองหน้าสัมผัส (เท่ากับ 1)

ผลรวมของสองหน้าสัมผัส (การทำงาน OR) จะเกิดขึ้นเมื่อมีการเชื่อมต่อแบบขนาน: มันถูกปิด (เท่ากับ 1) เมื่ออย่างน้อยหนึ่งหน้าสัมผัสที่เกิดวงจรถูกปิด (เท่ากับ 1)

ตรงกันข้ามของผู้ติดต่อนี้ (การดำเนินการไม่) เป็นผู้ติดต่อเท่ากับ 0 (เปิด) หากผู้ติดต่อนี้คือ 1 (ปิด) และในทางกลับกัน

เช่นเดียวกับพีชคณิตแบบบูลถ้าผู้ติดต่อถูกแทนด้วยตัวอักษร A และ B เราจะแสดงผลของสองผู้ติดต่อโดย A * B, ผลรวมโดย A + B, และการติดต่อข้าม A, โดย / A อธิบายไว้ในรูปที่ 1, 2 และ 3

ความถูกต้องของตารางที่สอดคล้องกับการดำเนินการ AND, OR และ NOT ตอนนี้ไม่มีใครสงสัย

ให้เราพักสองตัวอย่าง: 1 * 0 = 0 และ 1 + 0 = 1

สามารถเห็นได้จากรูปที่รายชื่อผู้ติดต่อที่ปิดอย่างถาวรที่เชื่อมต่ออยู่ในชุดที่มีรายชื่อผู้ติดต่อที่เปิดถาวรนั้นเทียบเท่ากับรายชื่อผู้ติดต่อที่เปิดถาวร (1 * 0 = 0) รายชื่อผู้ติดต่อที่ปิดถาวรอย่างต่อเนื่อง

เมื่อคุ้นเคยกับเลขคณิตของวงจรสัมผัสคุณสามารถอธิบายวงจรรีเลย์ด้วยสูตรโดยใช้หลักการประชุมที่ยอมรับได้ ในไซเบอร์เนติกส์สูตรดังกล่าวเรียกว่าโครงสร้าง

หากสูตรโครงสร้างของวงจรรีเลย์ใด ๆ เป็น 1 ดังนั้นสัญญาณสามารถผ่านได้ - วงจรจะปิด ในทางกลับกันถ้าสูตรโครงสร้างของวงจรเป็น 0 สัญญาณจะไม่ผ่านเลย - วงจรขาดสรุป: วงจรรีเลย์ทั้งสองมีค่าเท่ากันเมื่อสูตรโครงสร้างมีค่าเท่ากัน

ในการต่อเนื่องของบทความเราจะพิจารณาตัวอย่างของวงจรการติดต่อวงจรการติดต่อทั่วไปและรายการเทียบเท่ารวมถึงการวาดไดอะแกรมตามสูตรโครงสร้าง นอกจากนี้เรายังพิจารณาวงจรตรรกะหลักที่ทำหน้าที่ของพีชคณิตแบบบูล

ความต่อเนื่องของบทความ: พีชคณิตแบบบูล ส่วนที่ 3 แผนการติดต่อ

Boris Aladyshkin

Comments

[#1 อเล็กซ์]

ขอบคุณ

ย่อหน้าเดียวเท่านั้น:

"เช่นเดียวกับพีชคณิตแบบบูลถ้าผู้ติดต่อถูกแทนด้วยตัวอักษร A และ B เราจะแสดงผลของสองผู้ติดต่อโดย A * B, ผลรวมโดย A + B, และการติดต่อข้าม A, โดย / A อธิบายไว้ในรูปที่ 1, 2 และ 3 ..."

รูปที่ 3 อยู่ที่ไหน